회귀 알고리즘을 하나하나 자세히 공부하기 보기보다는 큰 틀에서 어떤 종류의 알고리즘이 있고,
어떤 특징이 있는지 대략적으로 공부하고자 작성했다.
회귀 알고리즘?
여러 개의 독립변수과 한 개의 종속변수 간의 상관관계를 모델링하는 기법
독립변수 : 영향을 미치는 요소
종속변수 : 영향을 받는 요소
| 독립변수 개수 | 회귀계수의 결합 |
| 1개 : 단일 회귀 | 회귀계수가 선형 : 선형회귀 |
| 여러개 : 다중 회귀 | 회귀계수가 비선형 : 비선형회귀 |
회귀 알고리즘의 종류
- 선형회귀 : 실제 값과 예측 값의 차이를 최소화하는 직선형 회귀선을 최적화하는 방식
- 일반 선형회귀
- 릿지(L2 규제)
- 라쏘(L1 규제, 피쳐 선택 기능)
- 엘라스틱넷(릿지+라쏘)
- 로지스틱 회귀
- 회귀 트리
단순 선형 회귀

하나의 특징(독립변수)을 가지고 라벨값(종속변수)을 예측하기 위한 회귀모델
가장 단순한 모델로 변수들의 관계를 일차식 y = ax + b의 형태로 만들어 최적의 a, b값을 찾아 선을 만든다.
최적의 a, b값을 찾기 위해서 경사 하강법을 이용한다.
다항 회귀

독립변수가 여러개인 경우 라벨값을 예측하기 위한 회귀모델
다항 회귀의 차수를 높일수록 = 독립변수가 많을수록 = 피쳐가 많을수록 과적합의 문제가 크게 발생할 수 있다.
릿지 Ridge
최적의 오차값을 구한 이후에 과적합을 개선하기 위해 회귀계수를 규제시켜 최선의 모델을 찾는 방법
회귀계수를 규제시킨다는 것은 조건을 건다는 것과 같은 의미

이 그래프에서 원래 최소오차값은 좌표에 찍여있는 검은색 점이다.
하지만 과적합을 해결하기 위해 초록색 원 모양의 규제(조건)을 추가했다.
최소 오차값이 초록색 원 모양에 들어오는 경우가 규제(조건)를 만족하면서 가질 수 있는 최소오차값이다.
규제를 만족하면서 가질 수 있는 최소오차값을 찾기위해 기존의 최소오차값(검은색 점)에서 오차범위를 점차 늘려(빨간색 타원) 규제(초록색원)와 만나는 지점을 찾는다.
릿지의 경우 규제를 걸 때 오차의 제곱값을 이용하기 때문에 2차식인 원의 모양으로 그래프에 표현하게 된다.
라쏘 Lasso
릿지와 비슷한 모델이지만 규제를 걸 때 오차의 절댓값을 이용한다는 점이 다르다.
절댓값을 이용하기 때문에 최소오차값이 0과 만나는 지점이 발생할 확률이 높고, 0이되면 해당 피쳐는 삭제된다.
이러한 특성 때문에 라쏘는 피쳐를 선택할 수 있는 기능이 있다고 본다.

릿지와 마찬가지로 최소오차값(검은색 점)이 있고, 규제(초록색 마름모)와 만날 수 있도록 오차범위(빨간색 타원)를 점진적으로 늘려가며 적합한 오차값을 찾는다. 라쏘의 경우 오차의 절댓값을 이용하기 때문에 절댓값함수에 의해 마름모꼴로 그래프에 표현된다.
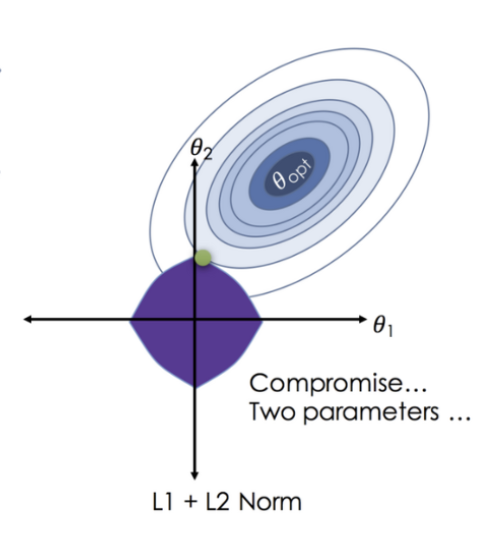
엘라스틱넷
릿지와 라쏘를 결합한 모델이다. 그래프로 표현하지면 다음과 같은 모양으로 표현할 수 있다.
로지스틱 회귀
로지스틱 회귀는 이름은 회귀이지만 실제로는 분류 알고리즘으로 사용된다.
시그모이드 함수의 최적선을 찾고 반환값을 확률로 간주해 확률에 따라 분류를 결정하는 분류 모델이다.
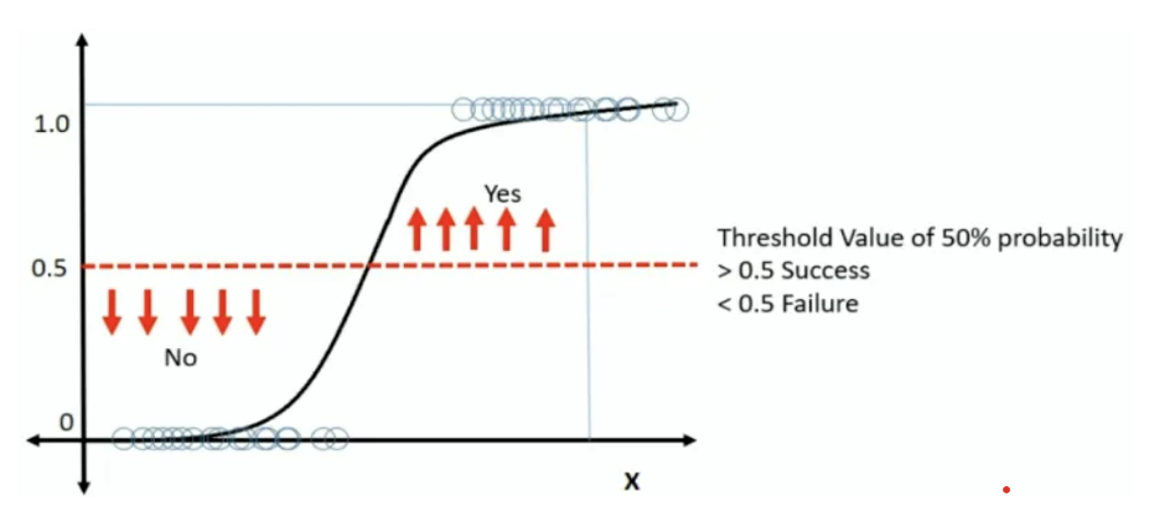
최적선이 0.5라고 한다면 회귀식에 따라 y 값이 0.5보다 작으면 조건에 해당되지 않음, 0.5보다 크면 조건에 해당됨으로 분류한다.
이 포스팅에서는 회귀식을 따로 설명하지는 않는다.
회귀 트리
지금까지는 선형 방식의 회귀 알고리즘을 봤다면 회귀트리는 선형방식이 아닌 트리방식의 회귀 알고리즘이다.
분류 트리와 비슷하지만 분류 트리는 Yes, No에 대해서 평가하는 반면 회귀트리는 각 데이터의 평균값(숫자값)을 구해 회귀 예측값을 계산단다.

'ML&DL > study' 카테고리의 다른 글
| 02. 경사하강법 Gradient Descent - 앤드류 응(Andrew Ng)교수님 머신러닝/딥러닝 한글자막 공부하기 (0) | 2021.08.13 |
|---|---|
| 01. Intro - 앤드류 응(Andrew Ng)교수님 머신러닝/딥러닝 한글자막 공부하기 (0) | 2021.08.09 |
| 파이썬 머신러닝 04-4. 분류 알고리즘 (앙상블 부스팅) (0) | 2021.08.03 |
| 파이썬 머신러닝 04-3. 분류 알고리즘 (결정트리, 앙상블 보팅, 배깅) (0) | 2021.07.30 |
| 파이썬 머신러닝 04-2. 언더피팅, 오버피팅과 해결방안 (0) | 2021.07.26 |

